Soal Trigonometri

Soal Trigonometri kelas 10

1. Untuk 0° ≤ x ≤ 360° tentukan himpunan penyelesaian dari sin x =  ½ …..

A. HP = {30o,120o}

B. HP = {30o,390o}

C. HP = {30o,480o}

D. HP = {120o,480o}

E. HP = {390o,480o}

Jawaban : A

Pembahasan : 

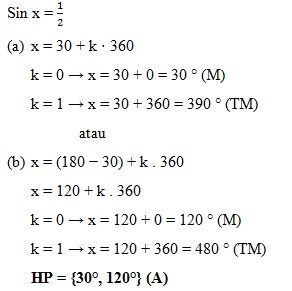
2. Untuk 0° ≤ x ≤ 360° tentukan himpunan penyelesaian dari cos x =  ½ ….

A. HP = {60o,420o}

B. HP = {60o,300o}

C. HP = {30o,360o}

D. HP = {30o,120o}

E. HP = {-60o,120o}

Jawaban : B

Pembahasan : 

3. Tentukan himpunan penyelesaian dari persamaan trigonometri sin x = sin 2/10 π, 0 ≤ x ≤ 2π …..

Jawaban : C

Pembahasan : 

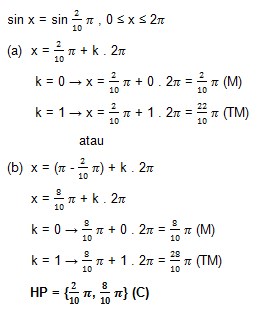
4. Tentukan nilai x yang memenuhi persamaan 2 sin x = 1 , dengan 0o ≤ x ≤ 360o …..

A. HP = {30o,390o}

B. HP = {150o,510o}

C. HP = {60o,390o}

D. HP = {30o,150o}

E. HP = {30o,60o}

Jawaban : D

Pembahasan : 

5. Untuk 0 ≤ x ≤ 2 π, tentukan himpunan penyelesaian dari persamaan tan (2x – ¼π) = ¼π , …..

10. Himpunan penyelesaian dari cos (x-15°) = ½√3 untuk 0o ≤ x ≤ 360o adalah…..

A. HP = {45o,315o}

B. HP = {45o,295o}

C. HP = {45o,345o}

D. HP = {75o,345o}

E. HP = {75o,315o}

Jawaban : E

Pembahasan : 

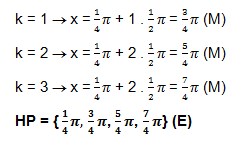
6. Tentukan himpunan penyelesaian dari persamaan sin2x – 2 sin x – 3 = 0 untuk 0o ≤ x ≤ 360o …..

A. HP = {-90o,270o}

B. HP = {-90o,270o, 630o}

C. HP = {-90o,630o}

D. HP = {270o}

E. HP = {90o}

Jawaban : D

Pembahasan : 

7. Himpunan penyelesaian persamaan cos 2x + 5 sin x + 2 = 0 untuk 0 ≤ x ≤ 2π adalah…..

Jawaban : E

Pembahasan : 

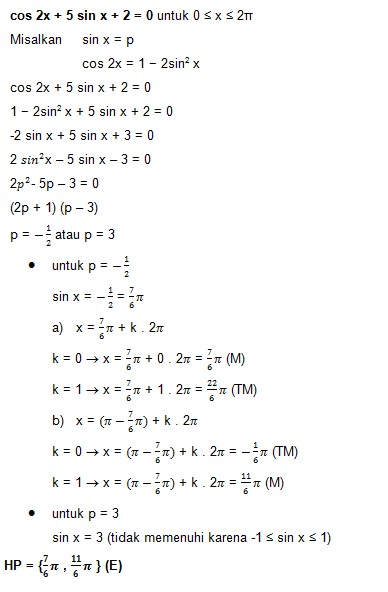
8. Nilai dari cos² 15° + cos² 35° + cos² 55° + cos² 75° adalah…

A. 2

B. -1

C. 1

D. -2

E. 3

Jawaban : A

Pembahasan : 

cos² 15° + cos² 35° + cos² 55° + cos² 75°

Rumus Kuadran I → sin α = cos (90-α) atau cos α = sin (90-α)

Identitas trigonometri → sin²α + cos²α = 1

= cos²15° + cos²35° + cos²55° + cos²75°

= cos²15° + cos²75° + cos²35° + cos²55°

= cos² (90-75)° + cos²75° + cos² (90-55)° + cos²55°

= sin²75° + cos²75° + sin²55° + cos²55°

= 1 + 1 = 2 (A)

9. Jika sin(x-600)° = cos(x-450)° maka nilai dari tan x adalah …..

A. √3

B. 1/3√3

C. 3 √3

D. 570o

E. 2 √3

Jawaban : B

Pembahasan : 

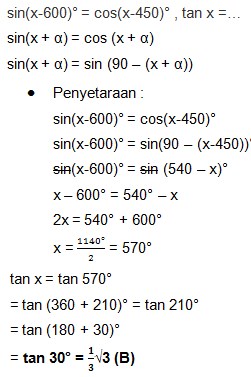
10. Himpunan penyelesaian dari cos (x-15°) = ½√3 untuk 0o ≤ x ≤ 360o adalah…..

A. HP = {45o,315o}

B. HP = {45o,295o}

C. HP = {45o,345o}

D. HP = {75o,345o}

E. HP = {75o,315o}

Jawaban : C

Pembahasan : 

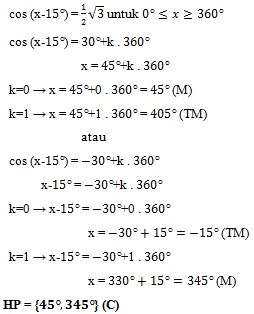
11.    Pada segitiga ABC lancip, diketahui cos A = 4/5 dan sin B = 12/13 maka sin C = ...
a.    20/65
b.    36/65
c.    56/65
d.    60/65
e.    63/65
Pembahasan:
Jika cos A = 4/5, maka: sin A = 3/5 (didapat dari segitiga siku-siku berikut ini:
(ingat ya, bahwa cos itu samping/miring dan sin itu depan/miring)

Jika sin B = 12/13 maka cos B = 5/13 (didapat dari segitiga siku-siku berikut ini:

Maka, sin C = sin A . cos B + sin B . cos A
                    = 3/5 . 5/13 + 12/13 . 4/5
                    = 15/65 + 48/65
                    = 63/65
Jawaban: E

12.    Nilai dari   = ...
a.    -2 - √3
b.    -1
c.    2 - √3
d.    1
e.    2 + √3
Pembahasan:

Jawaban: B

13.    Diketahui sin A = 12/13 dan cos B = 3/5, <A dan <B lancip. Nilai tan (A – B) = ...
a.    36/63
b.    26/63
c.    16/63
d.    6/33
e.    1/33
Pembahasan:
Sin A = 12/13, maka cos A = 5/13 (carilah dengan segitiga siku-siku seperti soal nomor 1)
Cos B = 3/5, maka sin B = 4/5 (carilah dengan segitiga siku-siku seperti soal nomor 1)

Jawaban: C

14.    Luas segitiga ABC adalah 24 cm2, sisi AC = 8 cm, dan AB = 12 cm. Nilai cos <A = ...
a.    1/3 √2
b.    ½
c.    1/3 √3
d.    ½ √2
e.    ½ √3
Pembahasan:
Perhatikan segitiga berikut:

Luas ABC = ½ . AB . AC . sin A
24 = ½ . 12 . 8 . sin A
24 = 48 sin A
Sin A = 24/48
Sin A = ½
A = 30
Maka cos A = cos 30 = ½ √3
Jawaban: E

15.    Diketahui segitiga PQR siku-siku di Q. Jika sin (Q + P) = r, maka cos P – sin R = ...
a.    -2r
b.    –r
c.    0
d.    R
e.    2r
Pembahasan:
sin (Q + P) = r
sinQ . cosP + sinP. cosQ = r
1.cos P + 0 = r (ingat ya, diketahui Q = siku-siku)
Cos P = r ... (i)
Sin R = sin (180 – (Q + P)
         = sin (Q + P)
         = r
Maka, cos P – sin R = r – r = 0
Jawaban: C

16.    Jika – π/2 < x < π/2 dan  maka cos x = ...
a.    ½ √3 dan 2/3√3
b.    – ½ √3 dan 2/3 √3
c.    ½ √3 dan – 2/3 √3
d.    – 1/3√2 dan – 2/3√3
e.    1/3√2 dan 2/3 √3
Pembahasan:

Misalkan sin x = A, maka:

    (2A – 1) (3A + 1) = 0
    A = ½ atau A = - 1/3
Maka, sin x = ½ , maka cos x = 1/2 √3  
           Sin x = - 1/3, maka cos x = 2/3√2
Jawaban: A

17.    Jika 0 ≤ x ≤ 2π dan 0 ≤ y ≤ 2π memenuhi persamaan sin (y + x) = sin y . cos x maka cosy . sin x = ...
a.    -1
b.    – ½
c.    0
d.    ½
e.    1
Pembahasan:
Sin (y + x) = sin y . cos x + cosy . sin x
sin y . cos x = sin y . cos x + cosy . sin x
cosy . sin x = sin y . cos x - sin y . cos x
cosy . sin x = 0
Jawaban: C

18.    Luas segi dua belas beraturan dengan panjang jari-jari lingkaran luar 12 cm adalah ...
a.    36 cm2
b.    36√3 cm2
c.    144 cm2
d.    432 cm2
e.    432√3 cm2
Pembahasan:
Yuk, ingat kembali rumus luas segi-n dengan panjang jari-jari lingkaran luar r:

Maka luas segi dua belas di atas adalah:

     L = 12 x ½ x 144 x sin 30
     L = 12 x 72 x ½
     L = 6 x 72
     L = 432 cm2
Jawaban: D

19.    Jika  dan q = sin x, maka p/q = ...
 
Pembahasan:


Jawaban: E

20.    Jika besar sudut dalam segi-8 beraturan adalah x maka sin x + cos x = ...
a.    0
b.    ½ √2
c.    – √2
d.    √2
e.    ¼ √2
Pembahasan:
Perhatikan segi-8 berikut ini:

< AOB = 360/8 = 45
<ABO = (180 – 45) : 2 = 67,5
Sudut segi-8 atau <ABC = <ABO +<OBC = 67,5 x 2 = 135
Maka nilai dari sin x + cos x = sin 135 + cos 135
                                           = sin (180 + 45) + (-cos (180 + 45)
                                           = sin 45 + (-cos 45)
                                           = ½ √2 - ½ √2
                                           = 0
Jawaban: A