PENERAPAN TURUNAN: KEMONOTONAN, INTERVAL FUNGSI NAIK/TURUN, KECEKUNGAN DAN UJI TURUNAN KEDUA

INTERVAL FUNGSI NAIK/TURUN, KEMONOTONAN, KECEKUNGAN DAN UJI TURUNAN KEDUA

Definisi Fungsi Naik Fungsi Turun

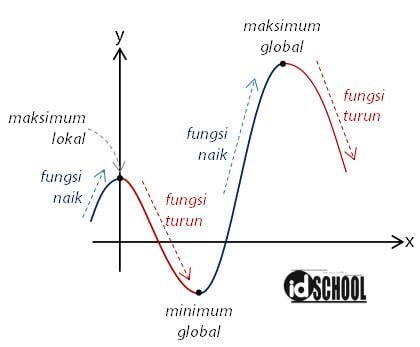
Persamaan suatu fungsi yang digambarkan dalam bidang koordinat dapat memiliki dua karakteristik yaitu fungsi naik dan fungsi turun. Suatu fungsi dikatakan naik jika absis (x) bergerak ke kanan maka grafik fungsi tersebut bergerak ke atas. Sedangkan fungsi dikatakan turun jika absis (x) bergerak ke kanan maka grafik fungsi tersebut bergerak ke bawah.

Antara fungsi naik dan fungsi turun dipisahkan oleh sebuah sebuah selang atau titik konstan. Selang atau titik konstan tersebut dapat berupa titik ekstrim atau titik stasioner, baik untuk nilai maksimum atau minimum. Ada empat titik stasioner yang dapat termuat dalam suatu kurva yaitu maksimum lokal, maksimum global, minimum lokal, atau minimum global.

Kesimpulan dari fungsi naik dan fungsi turun diberiakn seperti definisi berikut.

• Suatu fungsi f dikatakan fungsi naik pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) < f(x2).
• Suatu fungsi f dikatakan fungsi turun pada suatu selang jika untuk sembarang dua bilangan x1 dan x2 dalam selang tersebut, x1 < x2 mengakibatkan f(x1) > f(x2).

Beberapa fungsi akan selalu naik atau dapat juga selalu turun. Beberapa fungsi lain dapat naik pada selang tertentu dan turun pada selang yang lainnya. Contoh fungsi yang selalu naik adalah y = 2x, sedangkan contoh fungsi yang selalu turun adalah y = 2–x. Untuk contoh fungsi yang memiliki fungsi naik dan turun pada selang tertentu terdapat pada y = x2 (fungsi kuadrat).

Selanjutnya, sobat idschool akan mempelajari bagaimana cara menentukan Interval fungsi naik dan fungsi turun melalui ulasan di bawah.

Syarat Fungsi Naik dan Fungsi Turun

Cara menentukan interval fungsi naik dan fungsi turun dapat melalui sebuah teorema kemonotonan. 

Konsep Kemonotonan Fungsi

Sutau fungsi dikatakan monoton jika fungsi tersebut naik terus atau turun terus pada suatu selang atau interval. Jika fungsi f : S → R, S ⊆ R , maka  

• Fungsi f dikatakan naik jika ⩝ x₁ , x₂ ϵ S, x₁ < x_{2 →} f(x₁) < f(x₂)
• Fungsi f dikatakan turun jika ⩝ x₁ , x₂ ϵ S, x₁ < x₂ → f(x₁) > f(x₂)

Jika f adalah fungsi bernilai real dan dapat diturunkan pada setiap x ϵ I, maka

• Jika f ‘(x) > 0 maka fungsi selalu naik pada interval I.
• Jika f ‘(x) < 0 maka fungsi selalu turun pada interval I.
• Jika f ‘(x) ≥ 0 maka fungsi tidak pernah turun pada interval I.
• Jika f ‘(x) ≤ 0 maka fungsi tidak pernah naik pada interval I.

Teorma kemonotonan memuat hubungan antara turunan fungsi f(x) dan kriteria kurva atau fungsi, apakah naik atau turun. Pada teorema tersebut memuat syarat bagaimana suatu fungsi naik dan bagaimana syarat fungsi turun.

Dari teorema di atas dapat diperoleh dua kesimpulan. Pertama, hasil turunan positif (f’(x) > 0) akan mengakibatkan suatu fungsi naik. Kesimpulan kedua, hasil turunan negatif (f’(x) < 0) akan mengakibatkan fungsi tersebut turun. Selanjutnya, perhatikan penggunaan teorema tersebut untuk menyelesaikan contoh soal sederhana berikut.

Soal 1: Diketahui fungsi f(x) = −x2 − 4x + 12, interval f(x) naik dan interval f(x) turun terdapat pada ….

Jawab:

Menentukan Turunan f(x):
f ‘(x) = −2x − 4

Syarat fungsi f(x) naik: f ‘(x) > 0
−2x − 4 > 0
−2x > −4
x < −4/−2
x < 2

Syarat fungsi f(x) turun: f ‘(x) < 0
−2x − 4 < 0
−2x < −4
x > −4/−2
x > 2

Jadi, fungsi f(x) naik pada interval x > 2 dan f(x) turun pada interval x < 2.

Kecekungan

Karakteristik suatu fungsi yang naik atau turun dapat kita gunakan untuk mendeskripsikan grafik fungsi tersebut. Selain itu, apabila kita tahu dimana letak selang yang membuat f ’ naik atau turun maka kita dapat menentukan di mana grafik fungsi f akan cekung ke atas atau cekung ke bawah.

Definisi Kecekungan

Misalkan f terdiferensialkan pada selang buka I. Grafik f akan cekung ke atas pada I jika f ’ naik pada selang tersebut dan akan cekung ke bawah pada I jika f ’ turun pada selang tersebut.

Interpretasi grafis kecekungan dari suatu fungsi berikut akan sangat berguna.

1. Misalkan f terdiferensialkan pada selang buka I. Jika grafik f cekung ke atas pada I, maka grafik f berada di atas semua garis singgungnya pada selang tersebut. (Lihat gambar (a) di bawah).
2. Misalkan f terdiferensialkan pada selang buka I. Jika grafik f cekung ke bawah pada I, maka grafik f berada di bawah semua garis singgungnya pada selang tersebut. (Lihat gambar (b) di bawah).

Untuk menemukan selang buka di mana suatu grafik fungsi f cekung ke atas atau cekung ke bawah, kita harus menemukan selang di mana f ’ naik atau turun. Sebagai contoh, grafik

akan terbuka ke bawah pada selang buka (–∞, 0) karena

turun pada selang tersebut. Demikian pula, grafik f akan cekung ke atas pada selang (0, ∞) karena f ’ naik pada selang tersebut. Perhatikan gambar di bawah.

Teorema berikutnya menunjukkan bagaimana penggunaan turunan kedua suatu fungsi untuk menentukan selang di mana grafik f tersebut cekung ke atas atau cekung ke bawah. Bukti teorema ini merupakan akibat langsung dari Teorema Uji Fungsi Naik dan Turun, dan definisi kecekungan.

Teorema Uji Kecekungan

Misalkan f adalah suatu fungsi yang turunan keduanya ada pada selang buka I.

1. Jika f ”(x) > 0 untuk semua x dalam I, maka grafik f cekung ke atas pada I.
2. Jika f ”(x) < 0 untuk semua x dalam I, maka grafik f cekung ke bawah pada I.

Untuk menerapkan Teorema Uji Kecekungan, tentukan lokasi nilai-nilai x sedemikian sehingga f ”(x) = 0 atau f ” tidak ada. Gunakan nilai-nilai x tersebut untuk menentukan selang uji. Kemudian, ujilah tanda f ”(x) pada masing-masing selang uji.

Soal pilihan ganda dan pembahasannya yang berkaitan dengan penerapan Turunan

1. Fungsi f(x) = (x + 2)(x2 – 5x + 1) turun pada interval ….
A. –3 < x < 1
B. –1 < x < 3
C. –3 < x < 3
D. x < –3 atau x > 1
E. x < –1 atau x > 3

Pembahasan:

Diketahui:

• f(x) = (x + 2)(x2 – 5x + 1)
• Misalkan:
  u = x + 2 → du = 1 dx
  v = x2 – 5x + 1 → du = 2x – 5 dx

Menentukan turunan pertama fungsi f(x):
f’(x) = du/dx · v + dv/dx · u
f’(x) = 1 · (x2 – 5x + 1) + (2x – 5)(x + 2)
= x2 – 5x + 1 + 2x2 + 4x – 5x – 10
= 3x2 – 6x – 9

Syarat fungsi turun dipenuhi saat f’(x) < 0, sehingga dapat dibentuk sebuah pertidaksamaan 3x2 – 6x – 9 < 0.

Harga nol untuk turunan pertama fungsi f(x): f’(x) = 0
f’(x) = 0
3x2 – 6x – 9 = 0
x2 – 2x – 3 = 0
(x – 3)(x + 1) = 0
x1 = 3 atau x2 = –1

Uji nilai pada daerah-daerah yang dipisahkan oleh x1 = 3 dan x2 = –1 pada sebuah garis bilangan.

Untuk mendapatkan interval turun, akan dicari daerah yang menghasilkan nilai kurang dari 0 atau daerah dengan nilai negatif. Berdasarkan uji nilai seperti pada garis bilangan di atas dapat diperoleh bahwa daerah dengan nilai negatif terdapat pada selang interval –1 < x < 3.

Jadi, fungsi f(x) = (x + 2)(x2 – 5x + 1) turun pada interval –1 < x < 3.

Jawaban: B

2. Fungsi f(x) = 2x3 – 9x2 + 12x akan naik pada interval ….

A. x < –2 atau x > –1
B. –2 < x < –1
C. –1 < x < 2
D. 1 < x < 2
E. x < 1 atau x > 2

Pembahasan:

Turunan fungsi f(x):
f’(x) = 3 · 2x3–1 – 2 · 9x2–1 + 1 · 12x1–1
f’(x) = 6x2 – 18x + 12

Syarat fungsi f(x) naik:
f’(x) > 0
6x2 – 18x + 12 > 0

Selanjutnya adalah mencari himpunan penyelesaian dari pertidaksamaan 6x2 – 18x + 12 > 0.

Mencari titik-titik batas x (harga nol):
6x2 – 18x + 12 = 0
x2 – 3x + 2 = 0
(x – 2)(x – 1) = 0
x1 = 2 atau x2 = 1

Garis bilangan dan daerah yang memenuhi pertidaksamaan 6x2 – 18x + 12 > 0:

Jadi, fungsi f(x) = 2x3 – 9x2 + 12x akan naik pada interval x < 1 atau x > 2.

Jawaban: E

3. Diketahui , nilai dari f’(5) adalah ...

a.    6
b.    10
c.    14
d.    17
e.    20

PEMBAHASAN:

    f’(x) = 2x + 4
    f’(5) = 2(5) + 4
            = 14
JAWABAN: C

4.    Turunan pertama dari   adalah ...

PEMBAHASAN:


JAWABAN: D

5.    Diketahui  dan f’ adalah turunan pertama dari f. Nilai dari f’(1) = ...
a.    20
b.    21
c.    23
d.    23
e.    26

PEMBAHASAN:


               = 24 – 6 + 6 – 1
               = 23
JAWABAN: C

6.    Diketahui  dan f’ adalah turunan pertama f. Nilai f’(1) adalah ...

a.    3
b.    8
c.    13
d.    16
e.    21

PEMBAHASAN:


              = 3 – 20 + 25
              = 8
JAWABAN: B

7.    Diketahui . Jika f’ adalah turunan pertama dari f, maka nilai f’(x) = ...

PEMBAHASAN:
Kita gunakan rumus ini ya: 


JAWABAN: D


8.    Jika dengan f’ adalah turunan pertama f, maka nilai f’(2) adalah ...
a.    5
b.    20
c.    30
d.    40
e.    50

PEMBAHASAN:
Kita gunakan rumus ini ya: 


               = 20.1
               = 20
JAWABAN: B

9. Nilai maksimum dari fungsi  adalah ...
a.    8
b.    12
c.    16
d.    24
e.    32

PEMBAHASAN:
Nilai maksimum atau minimum suatu fungsi diperoleh jika f’(x) = 0
Maka:


Jadi, nilai maksimumnya adalah 12
JAWABAN: B

10. Turunan pertama fungsi  adalah f’(x). Nilai f’(1) = ...

a.    18
b.    24
c.    54
d.    162
e.    216

PEMBAHASAN:

Misalkan: 
               v = 2x – 1 -->  v’ = 2
Kita pakai rumus yang ini: f(x) = u.v --> f’(x) = u’.v + u.v’
Sehingga:

             = 18 . 9 . 1 + 27 . 2
             = 162 + 54
             = 216
JAWABAN: E