Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atau ![]() . Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
. Cara menghitung determinan matriks tergantung ukuran matriks bujur sangkar tersebut. Cara menghitung nilai determinan dengan ordo 3 akan berbeda dengan cara menghitung matriks bujur sangkar dengan ordo 2.
Untuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
matriks ordo 2 dinyatakan seperti bentuk di bawah.
![]()
Nilai determinan A disimbolkan dengan ![]() , cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
, cara menghitung nilai determinan A dapat dilihat seperti pada cara di bawah.
![]()
Contoh Soal:
Tentukan nilai determinan matriks
![]()
Pembahasan:
![]()
Determinan Matriks Ordo 3 x 3
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b6492567d55ede81657988571966a6ec_l3.png)
Cara menghitung determinan pada matriks dengan ordo tiga biasa disebut dengan Aturan Sarrus. Untuk lebih jelasnya, lihat penjelasan pada gambar di bawah.
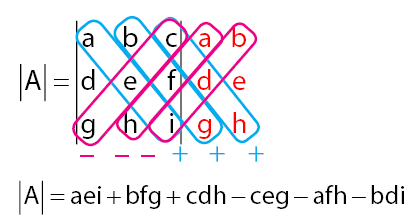
Contoh perhitungan determinan pada matriks ordo 3:
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a8947ae5b1c5dff0a86a995bd7c4f105_l3.png)
Maka,
![Rendered by QuickLaTeX.com \[ \left| \textrm{A} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ef53da91e11b43e4c90a06150a48d5bd_l3.png)
![]()
![]()
![]()
Selanjutnya, pembahasan kita akan berlanjut ke invers matriks.
Invers Matriks
Invers matriks dapat diartikan sebagai kebalikan dari suatu matriks tertentu. Jika suatu matriks bujur sangkar ![]() dikalikan terhadap inversnya yaitu matriks bujur sangkar
dikalikan terhadap inversnya yaitu matriks bujur sangkar ![]() maka menghasilkan matriks I (matriks identitas pada operasi perkalian matriks).
maka menghasilkan matriks I (matriks identitas pada operasi perkalian matriks).
Jika pada penjumlahan dua matriks, jumlah dua matriks bujur sangkar ![]() dan
dan ![]() akan menghasilkan matriks nol (matriks identitas pada operasi penjumlahan matriks).
akan menghasilkan matriks nol (matriks identitas pada operasi penjumlahan matriks).
![]()
![]()
Invers Matriks Ordo 2 x 2
Invers dari suatu matirks A
![]()
dinyatakan dalam rumus di bawah.
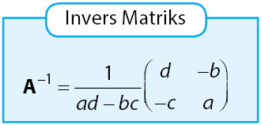
Contoh menentukan invers matriks A dapat dilihat seperti langkah-langkah berikut.
Diketahui:
![]()
Tentukan invers dari matrik A!
Pembahasan:
![]()
![]()
![]()
![]()
![]()
Invers Matriks Ordo 3 x 3
Cara untuk menentukan nilai invers matriks A dengan ordo 3 x 3 tidak sama dengan cara menentukan invers matriks dengan ordo 2 x 2. Cara menentukan invers matriks ordo 3 x 3 lebih rumit dari cara menentukan invers matriks 2 x 2. Simak ulasannyna pada pembahasan di bawah.
Sebelum menentukan invers matriks ordo 3 x 3, perlu dipahami terlebih dahulu mengenai matriks minor, kofaktor, dan adjoin. Simak penjelasannya pada uraian di bawah.
- Matriks Minor
Diketahui sebuah matriks A dengan ordo 3 seperti terlihat di bawah.
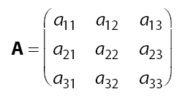
Matriks minor
 adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2 seperti persamaan di bawah.
adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2 seperti persamaan di bawah.
Matriks-matriks minor di atas digunakan untuk mendapatkan matriks kofaktor A.
- Kofaktor
Kofaktor baris ke-i dan kolom ke-j disimbolkan dengan
 dapat ditentukan dengan rumus seperti terlihat di bawah.
dapat ditentukan dengan rumus seperti terlihat di bawah.
Kofaktor di atas akan digunakan untuk menentukan adjoin matriks yang akan dicari nilai inversnya.
- Adjoin
Secara umum, sebuah matriks memiliki matriks adjoin seperti ditunjukkan seperti pada matriks di bawah.

Keterangan:
 adalah kofaktor baris ke-i dan kolom ke-j.
adalah kofaktor baris ke-i dan kolom ke-j.Sehinnga, adjoin dari matriks A dinyatakan seperti terlihat pada persamaan di bawah.
![Rendered by QuickLaTeX.com \[ Adj(A) \; = \; \; \begin{bmatrix} C_{11} & C_{21} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-e6eca1aeea0dde63e724e2223c823b34_l3.png)
- Invers Matriks
Bagian terakhir, bagian ini merupakan akhir dari proses mencari invers matriks dengan orde 3 atau lebih.
Matriks minor, kofaktor, dan adjoin yang telah kita bahas di atas berguna untuk menentukan nilai invers dari suatu matriks dengan ordo matriks di atas 3 atau lebih. Secara umum, cara menentukan invers matriks dapat diperoleh melalui persamaan di bawah.
![Rendered by QuickLaTeX.com \[ A^{-1} = \frac{1}{det(A)} \cdot Adj(A) \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3e41dfdc1f95ce9a6634dfd3c67a064f_l3.png)
Dengan substitusi nilai determinan matriks dan adjoin matriks maka akan diperoleh invers matriknya.
Agar lebih jelas, akan diberikan contoh soal cara mencari invers matriks berodo 3. Simak langkah-langkah yang diberikan di bawah.
Contoh soal menentukan invers matriks berordo 3 x 3
Tentukan invers matriks B yang diberikan pada persamaan di bawah.
![Rendered by QuickLaTeX.com \[ \textrm{B} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d98d58abc090d1db456f85de95b622bb_l3.png)
Pembahasan:
Menghitung nilai determinan B:
![Rendered by QuickLaTeX.com \[ \left| \textrm{B} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-4f990deb8c395fd9cff30afa053aa525_l3.png)
![]()
![]()
Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
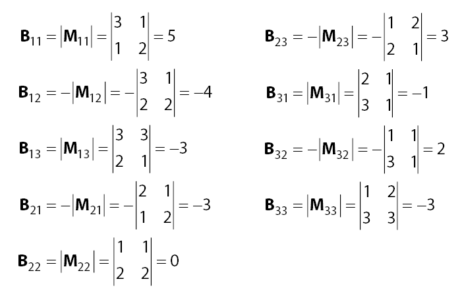
Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.
Menentukan Adjoin B:
Adjoin dari matriks B, sesuai dengan persamaan di atas akan diperoleh hasil seperti berikut.

Menentukan Invers Matriks B:
Persamaan umum untuk invers suatu matriks dinyatakan melalui persamaan di bawah.
![]()
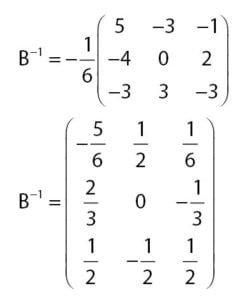
Sehingga, diperoleh invers matriks B seperti hasil berikut.

No comments:
Post a Comment