Definisi Turunan
Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel).
Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.
Menggunakan konsep limit yang sudah dipelajari, turunan dapat didefinisikan sebagai
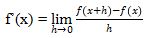
turunan tersebut didefinisikan sebagai limit dari perubahan rata-rata dari nilai fungsi terhadap variabel x.
Selanjutnya akan dijelaskan mengenai contoh penerapan turunan.
Penerapan Turunan
Berikut merupakan beberapa penerapan turunan.
- Turunan dapat diterapkan untuk menghitung gradien dari garis singgung suatu kurva.
- Turunan dapat digunakan untuk menentukan interval dimana suatu fungsi naik atau turun.
- Turunan dapat diterapkan untuk menentukan nilai stasioner suatu fungsi.
- Turunan dapat diterapkan dalam menyelesaikan permasalahan yang berkaitan dengan persamaaan gerak.
- Turunan dapat digunakan untuk menyelesaikan permasalahan maksimum-minimum.
Berikut ini akan dijelaskan mengena rumus turunan.
Rumus Turunan
Berikut merupakan beberapa rumus dasar untuk menentukan turunan.
- f(x) = c, dengan c merupakan konstanta
Turunan dari fungsi tersebut adalah f’(x) = 0.
- f(x) = x
Turunan dari fungsi tersebut adalah f’(x) = 1.
- f(x) = axn
Turunan dari fungsi tersebut adalah f’(x) = anxn – 1
- Penjumlahan fungsi: h(x) = f(x) + g(x)
Turunan fungsi tersebut yaitu h’(x) = f’(x) + g’(x).
- Pengurangan fungsi: h(x) = f(x) – g(x)
Turunan fungsi tersebut adalah h’(x) = f’(x) – g’(x)
- Perkalian konstanta dengan suatu fungsi (kf)(x).
Turunan fungsi tersebut adalah k . f’(x).
Berikut ini akan dijelaskan mengenai turunan fungsi.
Turunan Fungsi
Misalkan terdapat suatu fungsi f(x) = axn. Turunan dari fungsi tersebut yaitu f’(x) = anxn – 1.
Contohnya yaitu:
f(x) = 3x3
turunan dari fungsi tersebut yaitu
f’(x) = 3 (3) x3 – 1 = 9 x2.
Contoh lainnya misalnya g(x) = -5y-3.
Turunan dari fungsi tersebut adalah g’(y) = -5 (-3) y-3 – 1 = 15y-4.
Berikut akan dijelaskan turunan fungsi aljabar.
Turunan Fungsi Aljabar
Pembahasan turunan fungsi aljabar pada bagian ini meliputi turunan dalam bentuk perkalian dan turunan dalam pembagian fungsi aljabar.
Turunan fungsi aljabar dalam bentuk perkalian yaitu sebagai berikut.
Misalkan terdapat perkalian fungsi: h(x) = u(x) . v(x).
Turunan dari fungsi tersebut yaitu h’(x) = u’(x) . v(x) + u(x) . v’(x).
Keterangan:
- h(x) : fungsi dalam bentuk perkalian fungsi.
- h’(x) : turunan fungsi bentuk perkalian
- u(x), v(x) : fungsi dengan variabel x
- u’(x), v’(x) : turunan fungsi dengan variabel x
Turunan fungsi aljabar dalam bentuk pembagian yaitu:
Misalkan terdapat perkalian fungsi: h(x) = u(x)/v(x). Turunan dari fungsi tersebut adalah
h’(x) = (u’(x) . v(x) – u(x) . v’(x))/v2(x).
Keterangan:
- h(x) : fungsi dalam bentuk perkalian fungsi.
- h’(x) : turunan fungsi bentuk perkalian
- u(x), v(x) : fungsi dengan variabel x
- u’(x), v’(x) : turunan fungsi dengan variabel x
Turunan Akar
Misalkan terdapat suatu fungsi akar sebagai berikut
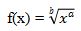
Untuk menentukan turunan dari fungsi tersebut, terlebih dahulu kita ubah ke dalam bentuk fungsi perpangkatan. Bentuk fungsi perpangkatannya yaitu f(x) = xa/b.
Turunan dari fungsi tersebut yaitu f’(x) = a/b . x(a/b) – 1.
Bagaimana jika fungsi berbentuk seperti ini?
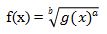
Untuk menentukan turunan fungsi di atas, terlebih dahulu diubah ke bentuk perpangkatan.
f(x) = g(x)z/b
Turunan dari fungsi tersebut yaitu f’(x) = a/b . g(x)(a/b) – 1 . g’(x).
Berikut ini akan dijelaskan mengenai turunan parsial.
Turunan Parsial
Apa itu turunan parsial? Turunan parsial merupakan suatu turunan dari fungsi peubah banyak terhadap suatu peubah, sedangkan peubah yang lain dipertahankan.
Misalkan terdapat suatu fungsi: f(x, y) = 2xy, turunan parsial dari fungsi tersebut terhadap variabel x yaitu fx’(x, y) = 2y.
Contoh lainnya yaitu, terdapat fungsi g(x, y) = -3xy2
Turunan parsial terhadap variable y yaitu fy’(x, y) = -6xy.
Berikutnya akan dijelaskan mengenai turunan implisit.
Turunan Implisit
Turunan implisit ditentukan berdasarkan variabel yang terdapat dalam fungsi.
Suatu fungsi dengan variabel x, turunannya : x d/dx.
Suatu fungsi dengan variabel y, turunannya : y d/dy. dy/dx.
Suatu fungsi dengan variabel x dan y, turunannya : xy d/dx + xy d/dy . dy/dx.
SIFAT SIFAT TURUNAN
Sifat-sifat Turunan
| 1. Jika dimana adalah konstanta, maka turunannya adalah |
| 2. Jika , maka turunannya adalah |
| 3. Jika maka turunannya adalah |
| 4. Jika maka turunannya adalah |
| 5. Jika maka turunannya adalah |
| 6. Jika maka turunannya adalah |
| 7. Jika maka turunannya adalah |
| 8. Jika maka turunannya adalah |
| 9. Jika maka turunannya adalah |
Sifat-sifat Turunan Logaritma Natural
| dimana adalah bilangan euler yang nilainya adalah |
Sifat-sifat Turunan Logaritma
| Perluasan Turunan Fungsi Trigonometri |
 , nilai dari f’(5) adalah ...
, nilai dari f’(5) adalah ...a. 6
b. 10
c. 14
d. 17
e. 20
PEMBAHASAN:

f’(x) = 2x + 4
f’(5) = 2(5) + 4
= 14
JAWABAN: C
2. Turunan pertama dari
 adalah ...
adalah ...
PEMBAHASAN:


JAWABAN: D
3. Diketahui
 dan f’ adalah turunan pertama dari f. Nilai dari f’(1) = ...
dan f’ adalah turunan pertama dari f. Nilai dari f’(1) = ...a. 20
b. 21
c. 23
d. 23
e. 26
PEMBAHASAN:


= 24 – 6 + 6 – 1
= 23
JAWABAN: C
4. Diketahui
 dan f’ adalah turunan pertama f. Nilai f’(1) adalah ...
dan f’ adalah turunan pertama f. Nilai f’(1) adalah ...a. 3
b. 8
c. 13
d. 16
e. 21
PEMBAHASAN:


= 3 – 20 + 25
= 8
JAWABAN: B
5. Diketahui
 . Jika f’ adalah turunan pertama dari f, maka nilai f’(x) = ...
. Jika f’ adalah turunan pertama dari f, maka nilai f’(x) = ...
PEMBAHASAN:
Kita gunakan rumus ini ya:



JAWABAN: D
6. Jika
 dengan f’ adalah turunan pertama f, maka nilai f’(2) adalah ...
dengan f’ adalah turunan pertama f, maka nilai f’(2) adalah ...a. 5
b. 20
c. 30
d. 40
e. 50
PEMBAHASAN:
Kita gunakan rumus ini ya:



= 20.1
= 20
JAWABAN: B
7. Jika f(x) = sin x cos 3x maka f’(π/6) = ...

PEMBAHASAN:
f(x) = sin x cos 3x
= ½ (sin 4x + sin (-2x))
= ½ sin 4x – ½ sin 2x
f’(x) = ½ . 4 cos 4x – ½ . 2 cos 2x
= 2cos 4x – cos 2x
Maka:
f’(π/6) = 2cos 4(π/6) – cos 2(π/6)
= 2.(- ½ ) – ½
= -1 – ½
= -1 1/2
JAWABAN: C
8. Jika
 , sin x ≠ 0 dan f’ adalah turunan f, maka f’(π/2) = ...
, sin x ≠ 0 dan f’ adalah turunan f, maka f’(π/2) = ...a. -2
b. -1
c. 0
d. 1
e. 2
PEMBAHASAN:

Misalkan: u = sin x + cos x --> u’ = cos x – sin x
v = sin x --> v’ = cos x
Ingat rumus ini ya:

Sehingga:


JAWABAN: B
9. Nilai maksimum dari fungsi
 adalah ...
adalah ...a. 8
b. 12
c. 16
d. 24
e. 32
PEMBAHASAN:
Nilai maksimum atau minimum suatu fungsi diperoleh jika f’(x) = 0
Maka:


Jadi, nilai maksimumnya adalah 12
JAWABAN: B
10. Turunan pertama dari fungsi
 adalah f’(x) = ...
adalah f’(x) = ...
PEMBAHASAN:

Misal: u = 1 + cos x --> u’ = – sin x
v = sin x --> v’ = cos x
Ingat rumus ini ya:

Sehingga:


JAWABAN: E
11. Turunan fungsi
 adalah ...
adalah ...
PEMBAHASAN:
 atau
atau 
Maka:

JAWABAN: B
12. Diketahui fungsi
 dan turunan pertama dari f adalah f’. Maka f’(x) = ...
dan turunan pertama dari f adalah f’. Maka f’(x) = ...a. 4 sin (2x + 3) cos (2x + 3)
b. -2 sin (2x + 3) cos (2x + 3)
c. 2 sin (2x + 3) cos (2x + 3)
d. -4 sin (2x + 3) cos (2x + 3)
e. sin (2x + 3) cos (2x + 3)
PEMBAHASAN:

f’(x) = 2 sin (2x + 3) . 2. cos (2x + 3)
= 4sin(2x + 3)cos(2x + 3)
JAWABAN: A
13. Grafik fungsi
 turun dalam interval ...
turun dalam interval ...a. x < -3 atau x > 1
b. x < -1 atau x > 3
c. x < -3 atau x > -1
d. -1 < x < 3
e. 1 < x < 3
PEMBAHASAN:
Syarat grafik f(x) turun adalah jika nilai f’(x) < 0, maka:


HP = -1 < x < 3
JAWABAN: D
14. Turunan pertama fungsi
 adalah f’(x). Nilai f’(1) = ...
adalah f’(x). Nilai f’(1) = ...a. 18
b. 24
c. 54
d. 162
e. 216
PEMBAHASAN:

Misalkan:

v = 2x – 1 --> v’ = 2
Kita pakai rumus yang ini: f(x) = u.v --> f’(x) = u’.v + u.v’
Sehingga:

= 18 . 9 . 1 + 27 . 2
= 162 + 54
= 216
JAWABAN: E
15. Turunan pertama dari y = sin 1/x adalah ...
a. cos x
b. sin 1/x
c. cos 1/x

PEMBAHASAN:

JAWABAN: E
 dalam ribuan rupiah. Agar biaya minimum maka harus diproduksi barang sebanyak ...
dalam ribuan rupiah. Agar biaya minimum maka harus diproduksi barang sebanyak ...a. 30
b. 45
c. 60
d. 90
e. 135
PEMBAHASAN:

Agar biaya minimum maka B’(x) = 0
B’(x) = 4x – 180
B’(x) = 0
4x – 180 = 0
4x = 180
x = 45
Jadi, agar biaya minimum maka harus diproduksi barang sebanyak 45
JAWABAN: B
17. Suatu proyek akan diselesaikan dalam x hari. Jika biaya proyek per hari adalah
 dalam ribuan rupiah maka biaya proyek minimum dalam x hari sama dengan ...
dalam ribuan rupiah maka biaya proyek minimum dalam x hari sama dengan ...a. Rp550.000,00
b. Rp800.000,00
c. Rp880.000,00
d. Rp900.000,00
e. Rp950.000,00
PEMBAHASAN:
 atau
atau 
Biaya minimum diperoleh ketika B’(x) = 0
B’(x) = 4x – 40
B’(x) = 0
4x – 40 = 0
4x = 40
x = 10
Subtitusikan x = 10 dalam persamaan

Jadi, biaya proyek minimum dalam x hari sama dengan Rp800.000,00
JAWABAN: B
18. Biaya produksi kain batik sepanjang x meter dinyatakan dengan fungsi
 ribu rupiah. Jika semua kain batik tersebut dijual dengan harga
ribu rupiah. Jika semua kain batik tersebut dijual dengan harga  ribu rupiah maka panjang kain batik yang diproduksi agar diperoleh laba maksimum adalah ...
ribu rupiah maka panjang kain batik yang diproduksi agar diperoleh laba maksimum adalah ...a. 15 m
b. 25 m
c. 30 m
d. 50 m
e. 60 m
PEMBAHASAN:
Laba = harga jual – harga produksi

Laba maksimum diperoleh ketika L’ = 0, maka:
L’ = 60 – 2x
L’ = 0
60 – 2x = 0
x = 30
Jadi, panjang kain batik yang diproduksi agar diperoleh laba maksimum adalah 30 m
JAWABAN: C
19. Sebuah roda setelah t detik berputar sebesar ѳ radian sehingga
 maka kecepatan sudut pada detik ke-3 adalah ...
maka kecepatan sudut pada detik ke-3 adalah ...a. 12 rad/ detik
b. 24 rad/ detik
c. 28 rad/ detik
d. 56 rad/ detik
e. 88 rad/ detik
PEMBAHASAN:

Kecepatan sudut = dѳ/dt = 128 – 24t
Kecepatan sudut pada detik ke-3 atau t = 3
128 – 24(3) = 128 – 72 = 56 rad/detik
JAWABAN: D
20. Rusuk suatu kubus bertambah panjang dengan laju 7 cm per detik. Laju bertambahnya volume pada saat rusuk panjangnya 15 cm adalah ...
a. 675 cm2/ detik
b. 1.575 cm2/ detik
c. 3.375 cm2/ detik
d. 4.725 cm2/ detik
e. 23.625 cm2/ detik
PEMBAHASAN:
r = panjang rusuk kubus
V = volume kubus
Laju pertambahan panjang rusuk kubus =

Laju pertambahan volume kubus adalah dV/dt
dV/dt = dV/ds x ds/dt
= 3r2 x 7
= 3. 152.7
= 4.725 cm2/ detik
JAWABAN: D
21. Grafik fungsi kuadrat
 menyinggung garis y = 3x + 4. Nilai b yang memenuhi adalah ...
menyinggung garis y = 3x + 4. Nilai b yang memenuhi adalah ...a. -4
b. -3
c. 0
d. 3
e. 4
PEMBAHASAN:
Gradien garis singgung grafik
 adalah f’(x) = 2x + b
adalah f’(x) = 2x + bGaris singgungnya y = 3x + 4 memiliki gradien m = 3, maka:
2x + b = 3 ... (i)
Titik singgungnya adalah:
 = 3x + 4
= 3x + 4x2 + (b - 3)x = 0
x(x + (b – 3)) = 0
x = 0 atau x = b – 3 ... (ii)
Subtitusikan (ii) ke (i):
2(b – 3) + b = 3
2b – 6 + b = 3
3b = 9
b = 3
JAWABAN: D
22. Jumlah dua bilangan positif x dan y adalah 18. Nilai maksimum x.y adalah ...
a. 100
b. 81
c. 80
d. 77
e. 72
PEMBAHASAN:
x + y =18 --> x = 18 – y
x.y = (18 – y)y
= 18y – y2
x.y mencapai nilai maksimum jika(x.y)’ = 0
(x.y)’ = 18 – 2y
(x.y)’ = 0
18 – 2y = 0
2y = 18
y = 9
x = 18 – y --> 18 – 9 = 9
Nilai maksimum x.y adalah 9 . 9 = 81
JAWABAN: B
23. Persamaan garis singgung yang menyinggung kurva
 di titik (-1, 0) adalah ...
di titik (-1, 0) adalah ...a. y = -x + 1
b. y = x + 1
c. y = x – 1
d. y = 6x + 6
e. y = 6x – 6
PEMBAHASAN:
Gradien kurva
 adalah
adalah 
Menyinggung suatu garis di titik (-1, 0) maka:


y’ = 1 atau m = 1
Maka persamaan garisnya:
y – y1 = m (x – x1)
y - 0 = 1 (x + 1)
y = x + 1
JAWABAN: B
24. Jika garis singgung pada kurva
 di titik yang berabsis 1 adalah y = 10x + 8 maka a = ...
di titik yang berabsis 1 adalah y = 10x + 8 maka a = ...a. 6
b. 7
c. 8
d. 9
e. 10
PEMBAHASAN:
 memiliki gradien (m): y’ = 2x + a
memiliki gradien (m): y’ = 2x + aGaris singgungnya memiliki absis 1, maka:
y’ = 2.1 + a
y’ = 2 + a
Persamaan garis singgungnya adalah y = 10x + 8, memiliki gradien (m) = 10
2 + a = 10
a = 8
JAWABAN: C
25. Keliling persegi panjang (2x + 20) dan lebar (8 – x). Agar luas persegi panjang maksimum maka panjangnya ...
a. 10
b. 9
c. 4,5
d. 3,5
e. 3
PEMBAHASAN:
Misalkan panjang persegi panjang = p
Keliling = 2 (p + l)
(2x + 20) = 2(p + (8 – x))
x + 10 = p + (8 – x)
2x + 2 = p
Luas persegi panjang:
L(x) = p.l
= (2x + 2) (8 – x)

Luas akan maksimum ketika L’(x) = 0, maka:
L’(x) = -4x + 14
L’(x) = 0
-4x + 14 = 0
4x = 14
x = 3,5
Maka panjangnya: 2x + 2 = 2(3,2) + 2 = 9
JAWABAN: B

No comments:
Post a Comment